선형대수 기본 - 벡터
Linear Algebra - Essence of linear algebra(Vector)
벡터 개념의 필요성
최근 정보검색, 데이터과학기초(Fundementals of data science)과목을 수강하면서 벡터의 중요성을 깨닫게 되었습니다. 정보검색에서 document와 query의 similarity를 측정하기 위해 벡터가 필요하였고, 데이터과학기초에서는 Supervised learning 범주에 속하는 SVM(Support Vector Machine)에서 벡터 개념이 필요하였습니다. 지난학기 벡터 개념이 제대로 정립이 되어있지 않아 공부하는데 어려움이 있었던 경험을 계기로 이번 포스팅을 작성하게되었습니다.
출저를 먼저 밝히자면 유튜브 Blue1Brown 채널의 선형대수 시리즈 영상을 보며 정리했음을 알립니다.
벡터 개요
기본적으로 선형 대수의 구성요소는 벡터입니다. 따라서 선형대수의 기본 구성요소인 벡터에 대해 명확히 알고가는것은 중요한 일 일것입니다.
벡터는 물리학, 수학, CS분야에서 뜻하는바가 조금씩 다릅니다. 이번 포스팅에서는 CS분야에 사용되는 벡터에 대해 중점적으로 기술하겠습니다.
CS관점에서 Vector가 의미하는 바는 순차 숫자 리스트입니다. 예를들어 한화를 기준으로 비트코인에 대한 정보를 2차원(길이가 2인) 벡터로 모델링 해본다면 다음과 같습니다.
1은 비트코인의 수량을 뜻합니다. 즉 비트코인 1개당 4500만원이라는 정보를 모델링 하고 있는것 입니다.

우리는 기하학 관점에서 벡터를 원점에 뿌리를 둔 화살표라고 생각하면 벡터를 이해하기 수월할 것 입니다. 이는 벡터는 원점이 아닌 다른 좌표에 벡터를 표시할 수 있는 물리학 관점과 달리 선형대수학에서는 기본적으로 벡터는 원점에 뿌리를 둔 벡터라고 생각하면 이해하기 편합니다. CS관점에서 우리는 숫자-리스트라는 관점으로 벡터를 이해 해보려고 합니다. 숫자리스트는 곧 벡터의 좌표를 의미합니다.
벡터의 좌표는 숫자쌍입니다. 이 숫자쌍은 꼬리(원점)에서 시작한 벡터가 끝에 어떻게 다다를지 알려줍니다. 첫 번째 숫자는 원점을 기준으로 x축을 따라 얼마나 떨어졌는지가에 대한 정보를 포함하고 양수면 오른쪽, 음수면 왼쪽을 의미합니다. 마찬가지로 두번 째 숫자의 경우 y축에 대한 좌표 정보를 가집니다. 마찬가지로 양수이면 위쪽 음수이면 아래쪽을 의미하게됩니다.
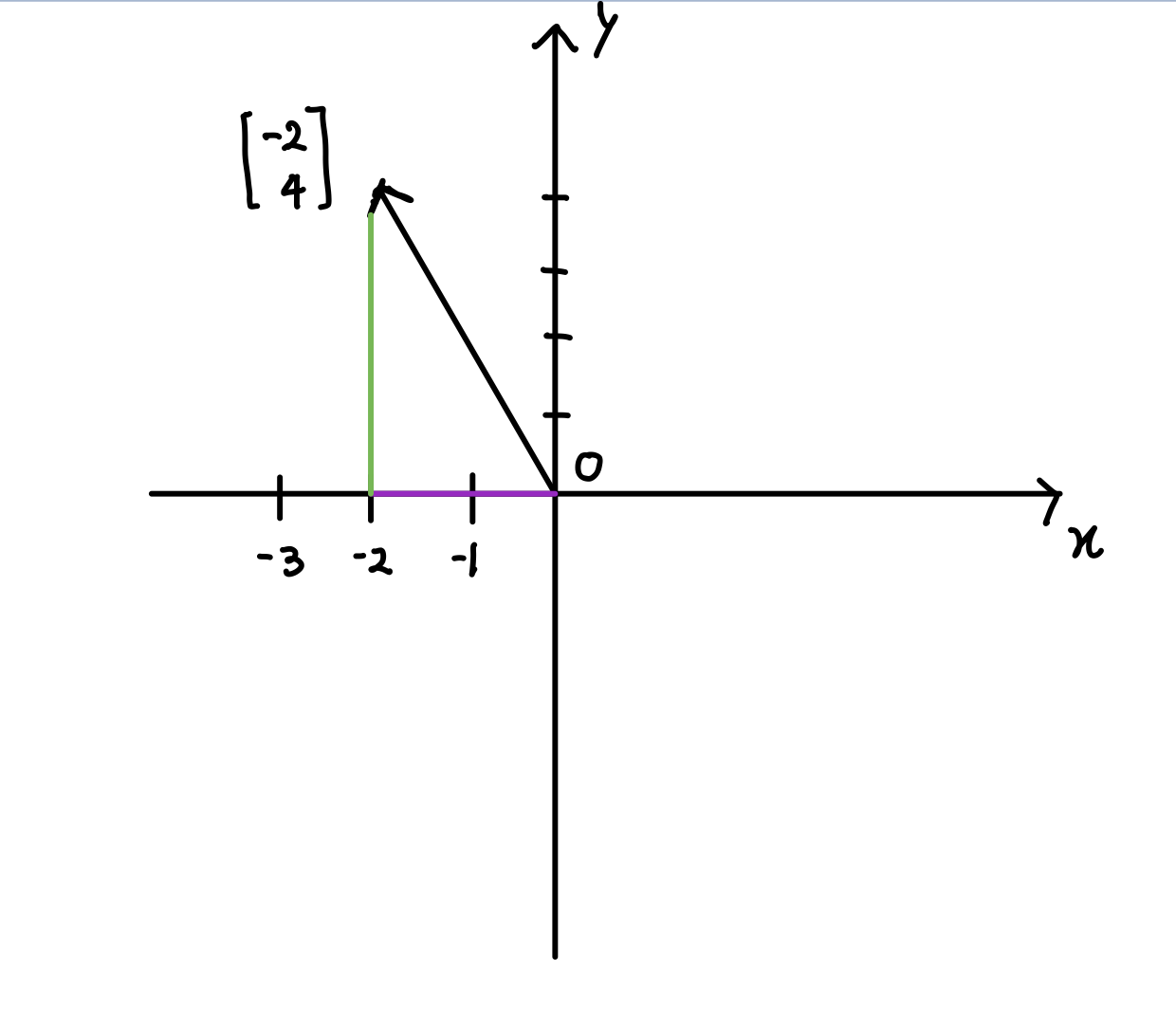
위 그림에서 첫번째 원소(-2)는 x축에 평행하면서 -2만큼 이동하라는 의미이고, 두번째 원소(4)는 y축과 평행하여 4만큼 이동하라는 뜻입니다. 이는 3차원,4차원…n차원으로 확장가능한 개념이며, 3차원까지는 우리가 간단하게 시각화를 할 수 있지만 그 이상의 차원은 상상해보기가 힘듭니다.
\[\begin{bmatrix}2\\3\\5\end{bmatrix},\begin{bmatrix}2\\3\\5\\7\end{bmatrix} ...\]벡터의 연산
벡터의 합
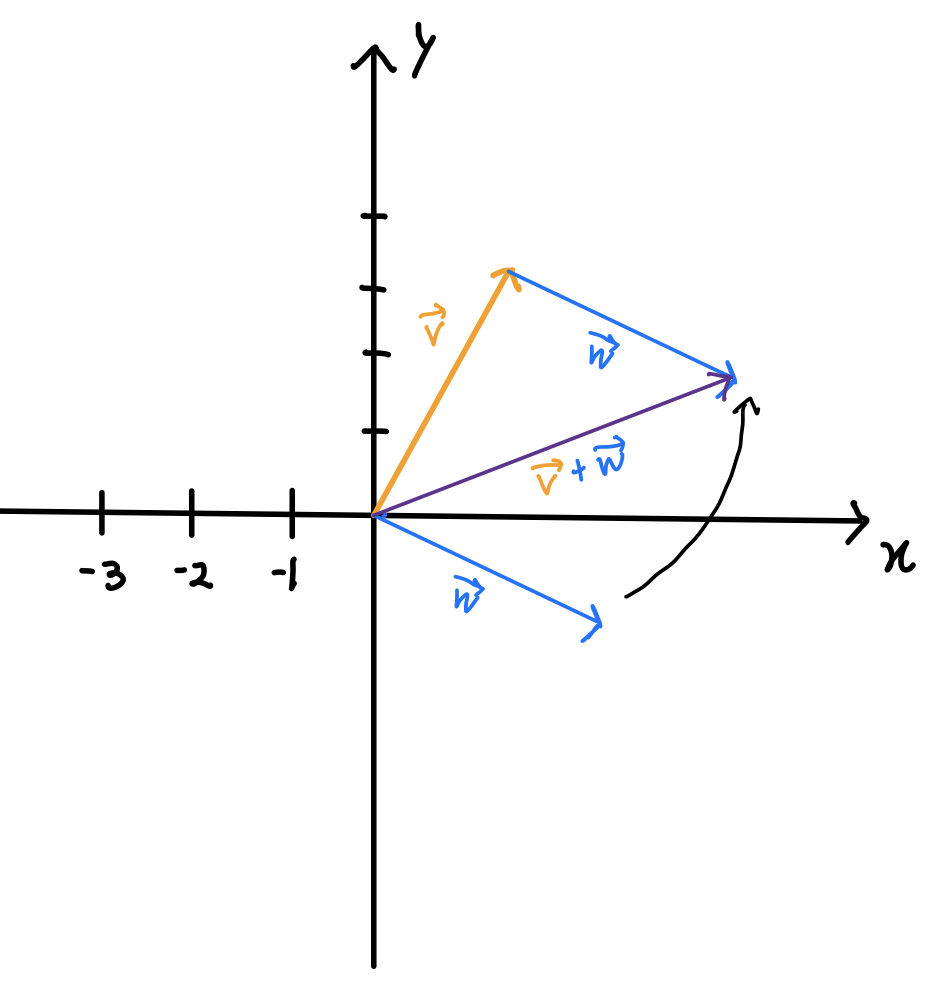
결국 선형대수의 모든 주제는 덧셈과, 곱셈 두가지 연산을 중심으로 일어납니다. 덧셈에 대해 먼저 논해보자면 아래와 그림과 같이 두 벡터가 있다고 가정해봅시다. 벡터v는 오른쪽 위쪽을 향한 벡터이고 벡터w는 오른쪽 아랫방향을 가리키고 있습니다. 이 두 벡터를 더하는 행위는 한 벡터의 꼬리를 다른 벡터의 끝으로 옮기는것을 말합니다.
그리고나서 벡터v의 꼬리부분에서 옮겨진 벡터w의 끝을 가리키는 새 벡터를 그리면 바로 이 새 벡터가 두 벡터의 합을 나타냅니다. 흥미로운 부분은 선형대수에서 유일하게 벡터를 원점으로부터 멀리 이탈시키는 순간이라는 점입니다.
\[\]
벡터의 덧셈을 좀 더 간단히 생각해보면 아래 그림과 같이 생각해볼 수 있습니다.
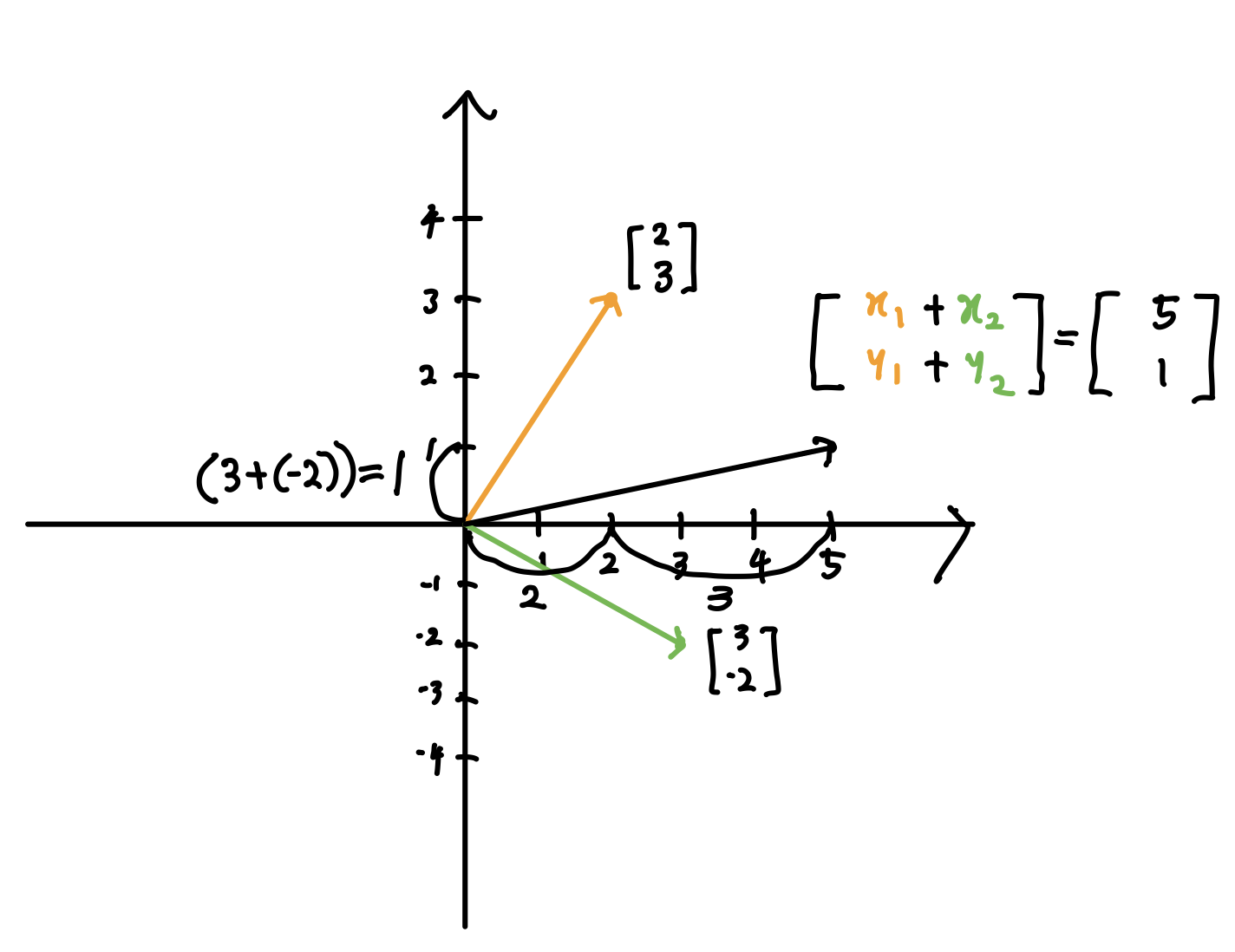
단순히 벡터의 합을 각 벡터의 원소에 대응하는 숫자의 합이라고 생각하면 이해하기 쉽습니다. 즉 두 벡터의 합으로 생성된 새 벡터는 두 벡터의 x좌표 정보를 나타내는 원소의 합(2+3=5) y좌표 정보를 나타내는 원소들의 합(3+(-2))로 새 벡터를 나타낼 수 있습니다. 원점을 기준으로 x축의 방향 5칸 이동, y축의 방향으로 1칸이동한 위치에 점을 찍고 화살표를 그림으로 써 동일한 결과를 얻을 수 있습니다.
벡터의 곱(스칼라 곱)
벡터의 곱은 합보다 더욱 간단합니다.
\[2*\begin{bmatrix}2\\3\end{bmatrix}=\begin{bmatrix}4\\6\end{bmatrix}\]어떤 벡터의 각 원소에 Scalar(Number)를 곱하면 그것이 곧 벡터의 곱이됩니다. 기하학적으로 생각하면 벡터를 Scalar만큼 늘리거나 줄이는 것에 해당합니다. 벡터를 늘리는 연산은 위와같이 분수가 아닌 정수 형태의 곱으로 나타나고 줄이는 연산은 분수형태의 Scalar가 곱해지게됩니다. 음수의 경우도 생각해 보아야하는데요, 음수의 경우는 벡터의 방향을 현재 벡터의 정 반대의 방향을 가지는 벡터로 변환하는 기능을 합니다. 아래의 벡터의 스칼라 곱 연산을 시각화 해본 그림입니다.
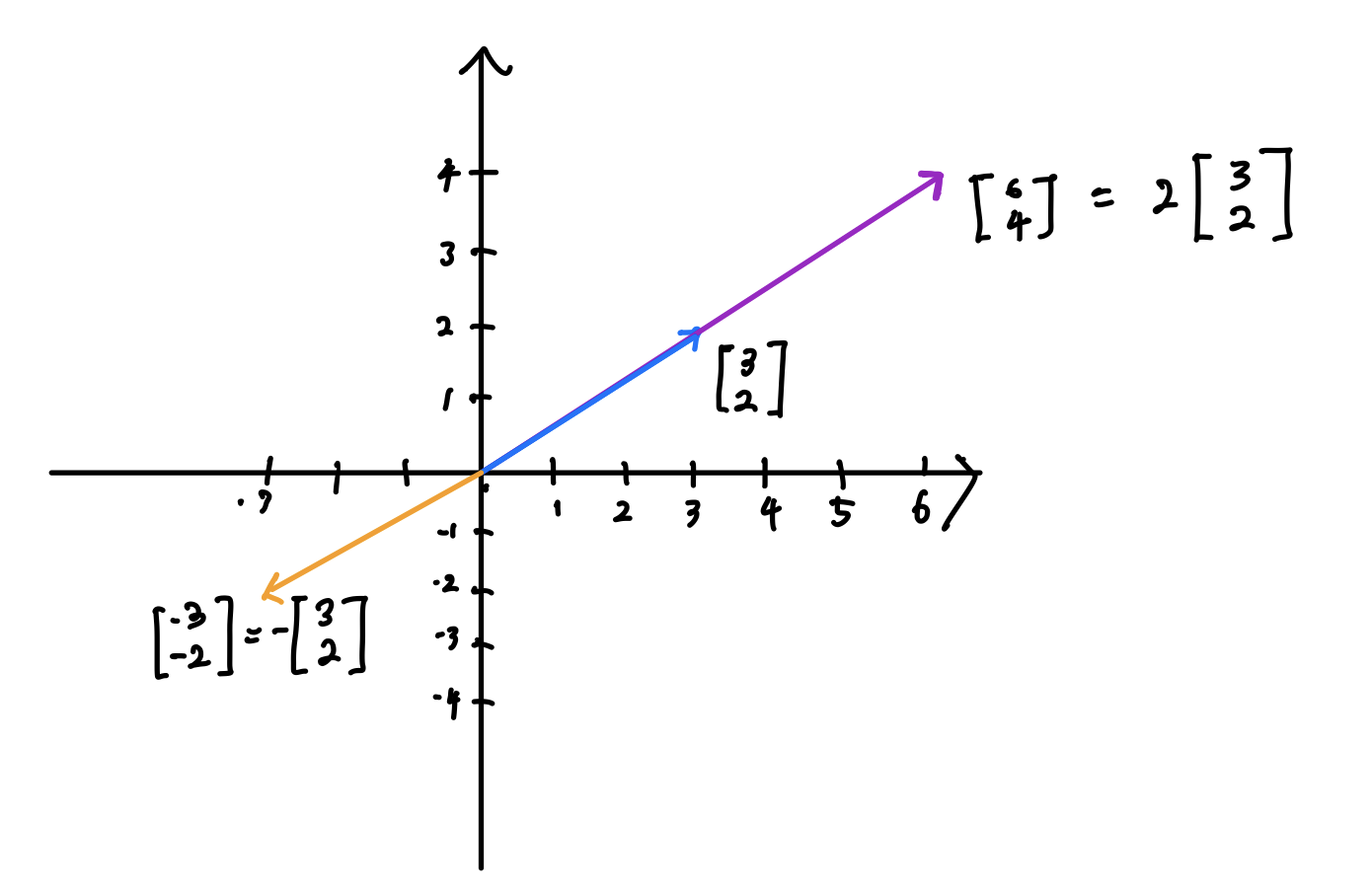

Leave a comment